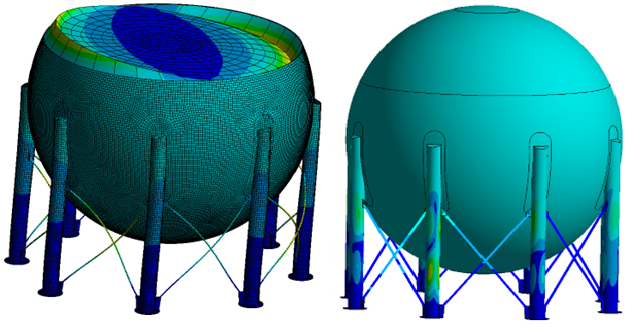
На основе анализа существующих подходов к оценке надежности стареющего оборудования и конструкций, сложившихся в различных отраслях промышленности, выявлены общие проблемы традиционных расчетных методов, обусловленные несовершенством поверочных расчетов на прочность. Исходя из этого, рассматривается новая методология оценки надежности конструкций с применением компьютерного статистического моделирования на базе расчетного процессора NX™ Nastran системы NX™ Advanced Simulation компании Siemens PLM Software.
В настоящее время метод конечных элементов является одним из самых эффективных методов решения многочисленных инженерных задач с помощью ЭВМ. Программные комплексы (системы инженерного анализа), построенные на базе метода конечных элементов, позволяют в естественной и физически наглядной форме учитывать сложность геометрии и граничных условий, реальные нагрузки, свойства материала и другие параметры конструкции.
Различные виды анализа, выполняемые с применением систем инженерного анализа, основаны на классических инженерных подходах к разработке математических моделей поведения изделия при различных воздействиях. В конечно-элементной постановке задачи моделирования исследуемая область предварительно разбивается на ограниченное множество конечных элементов, связанных между собой на уровне узлов. Искомыми переменными уравнений математических моделей являются перемещения, повороты, температура, давление, скорость, потенциалы электрических или магнитных полей. Эти переменные определяют степени свободы узлов. Их конкретное содержание зависит от типа конечного элемента, который связан с данным узлом. Например, в задачах прочностного анализа для каждого элемента с учетом степеней свободы его узлов могут быть сформированы матрицы жесткости. Множество степеней свободы, определяющих состояние всей системы в данный момент времени, называется волновым фронтом. После прохождения волнового фронта через все элементы и вычисления всех искомых переменных можно анализировать полученные результаты и строить гипотезы о поведении исследуемого изделия.
Другой класс задач — задачи оценки надежности конструкций. Данный класс задач появляется тогда, когда необходимо учесть: стохастичность механических свойств материалов конструкции, случайность геометрических характеристик, нагрузки вероятностного характера. Рассмотрим общую методологию решения задач оценки надежности, при этом в качестве системы инженерного анализа выберем систему NX™ Advanced Simulation на базе расчетного процессора NX™ Nastran.
При оценке надежности с применением численных методов и NX Nastran конструкция представляется как трехмерная модель с фиксированным числом определяющих параметров, каждый из которых задан в виде статистического ряда чисел (вариационного ряда).
Для примера рассмотрим модель трубопроводной конструкции. Номинальные значения основных определяющих параметров конструкции следующие:
- наружный диаметр Dн=1220 мм;
- номинальная толщина стенки δн = 12 мм;
- нормативное сопротивление растяжению (сжатию) металла (предел текучести) R2Н =362.6 МПа (сталь 17Г1С);
- рабочее давление Р=5.4 МПа.
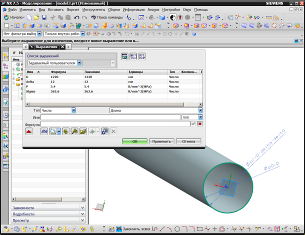
Рис. 1
Таблица 1 — Вариационные ряды определяющих параметров
| Определяющий параметр | Объем выборки | ||||
| 1 | 2 | 3 | 4 | 5 | |
| Толщина стенки δн, мм | 11,997 | 12 | 12,001 | 12,002 | 12,003 |
| Наружный диаметр Dн , мм | 1219,75 | 1219,9 | 1220 | 1220,15 | 1220,35 |
| Рабочее давление Р, МПа | 5,2 | 5,35 | 5,43 | 5,47 | 5,61 |
| Предел текучести R2Н, МПа | 348,1 | 356,2 | 364,3 | 367,5 | 377,5 |
Для проведения оценки надежности конструкции на первом этапе в СAD модуле системы NX™ (модуль Modeling) строится параметрическая трехмерная модель с учетом определяющих параметров заданных пользователем (рис. 1).
В качестве определяющих параметров заданных пользователем выступают следующие случайные величины (определяющие параметры имеющие разброс, заданный в виде соответствующих вариационных рядов в таблице 1):
Dн — наружный диаметр конструкции;
δн (Delta) — толщина стенки;
R2Н (Sigma) — характеристика материала конструкции: предел текучести (сталь 17Г1С);
Р — нагрузка в виде давления.
На втором этапе строится конечно-элементная модель (КЭМ) и расчетная модель (РМ) конструкции. КЭМ ассоциирована с геометрией параметрической трехмерной модели и построена на базе объемных конечных элементов (КЭ) второго порядка (рис. 2). Сетка (КЭ) ассоциирована с геометрической моделью (рис. 1), соответственно параметры D, Delta относятся к геометрии конструкции, а параметр Sigma задается на уровне создания физических свойств КЭ. На уровне физических свойств также задаются детерминированными следующие механические характеристики материала: модуль упругости, коэффициент Пуассона, плотность. Нагрузка (параметр P) задается на уровне определения начальных и граничных условий в РМ, которая ассоциирована с КЭМ.
На третьем этапе следует определить «слабейшее звено конструкции» — узел с максимальными напряжениями при номинальных значениях основных определяющих параметров. Для этого проводим статический расчет с применением расчетного процессора NX Nastran. Параметры расчета показаны на рис. 3.
Максимальные напряжения оцениваем по критерию Мизеса (Von-Mises), и в данном случае наиболее нагруженная область получается в узле № 107204 (рис. 4).
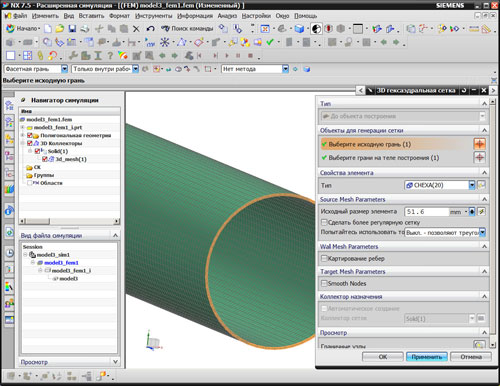
Рис. 2
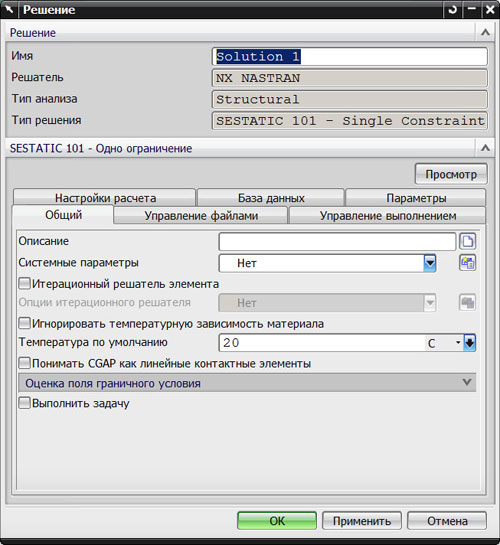
Рис. 3
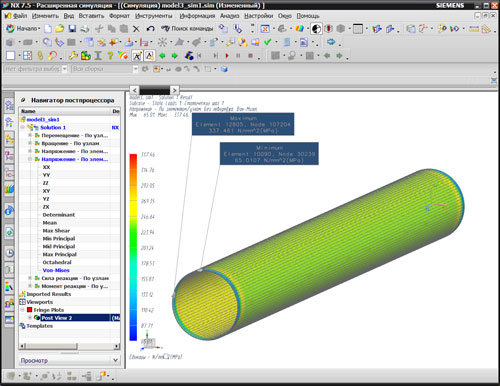
Рис. 4
Для решения следует многократно запустить статический расчет КЭМ конструкции с учетом данных статистического ряда каждого из определяющих параметров (таблица 1). Алгоритм представляет собой вложенный цикл по статистическим рядам определяющих параметров.
В теле цикла средствами NX™ Nastran производится расчет конечно-элементной модели с текущими значениями параметров из соответствующего статистического ряда. Реализация такого алгоритма обычно производится языком команд системы инженерного анализа. Используя команды системы, составляется управляющая программа для многократного запуска расчетного процесса. В случае системы NX™ (модуль Advanced Simulation) используется специализированная программа на языке VB.NET для пользовательского интерфейса и управляющая программа на языке DMAP. Язык DMAP — это язык программирования NX™ Nastran, доступный как дополнительный модуль и позволяющий пользователям расширять возможности NX™ Nastran путем написания собственных модулей и приложений. Пользовательский интерфейс разрабатывается с применением визуального программирования в соответствующем модуле Dlock UI Styler (рис. 6).
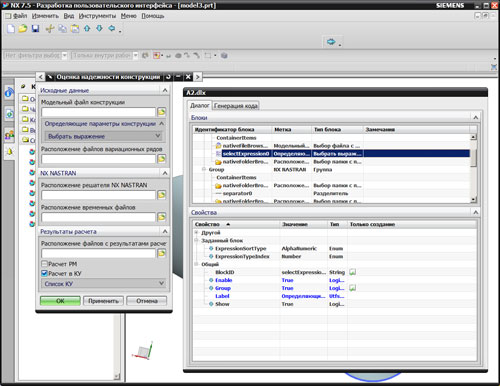
Рис. 6
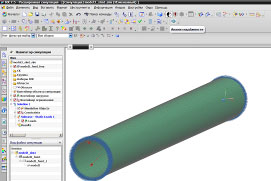
Рис. 7
1) Параметрическая трехмерная модель в виде файла *.prt. При этом в пользовательском интерфейсе следует указать расположение модельного файла. В этом же каталоге должны быть сохранены ассоциированные КЭМ (файл *. fem) и РМ (файл *.sim).
2) Вариационные ряды определяющих параметров в виде файлов *.txt. Файлы вариационных рядов являются стандартными текстовыми файлами и могут быть созданы с применением редактора «Блокнот». Имена данных файлов должны соответствовать наименованию определяющих параметров. В нашем случае: D.txt, Delta.txt, Sigma.txt, P.txt.
3) Данные по расположению решателя NX™ Nastran и расположению временных файлов в виде соответствующих путей к каталогам на жестком диске компьютера.
4) Данные по расположению на жестком диске компьютера файлов результатов расчета, файлов шаблонов MS Excel и номера контрольных узлов (КУ) в которых будет произведен расчет надежности.
Таким образом, на четвертом этапе следует запустить пользовательский интерфейс (рис. 8), ввести исходные данные и запустить расчет выбрав команду «ОК». В нашем случае расчет будет произведен для узла с максимальными напряжениями. Номер узла задается в соответствующем списке (рис. 9).
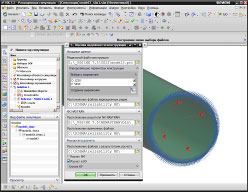
Рис. 8
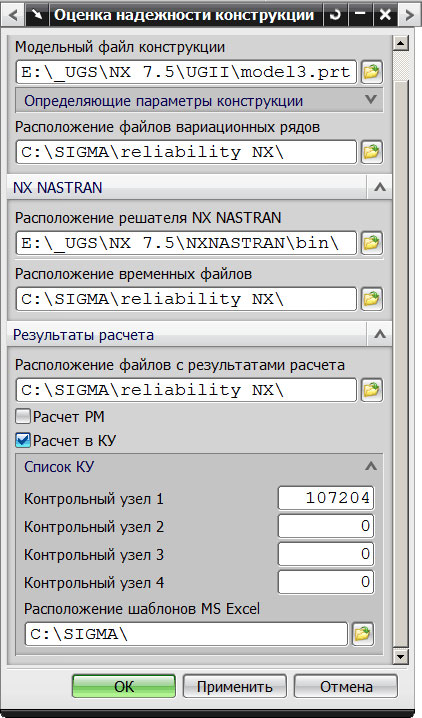
Рис. 9
по приведенному алгоритму. Данные 
представляются как эмпирические распределения для заданного узла конечно-элементной модели и сохраняются в виде таблиц MS Excel. Дальнейший расчет надежности производится в рамках шаблона MS Excel по методу определения вероятности безотказной работы (надежности) при эмпирических распределениях R и Q. Данный метод вычисления надежности приведен в специальной литературе (K.C. Kapur, L.R. Lamberson «Reliability in Engineering Design», Department of Industrial Engineering and Operations Research Wayne State University Detroit, Michigan 48202) и используется тогда, когда нет оснований для принятия допущения о каком-либо конкретном распределении нагрузки Q или несущей способности R, но имеется достаточный объем эмпирических данных. В нашем случае в качестве эмпирических данных выступают данные вычислительного эксперимента — результаты расчета КЭМ в теле цикла. Вводя обозначения 
и 
, запишем выражение для вероятности безотказной работы конструкции или надежности:
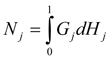
Nj = 0,9287.
Все вычисления и построения кривых производятся автоматизировано в рамках шаблона MS Excel.
Расчет может производиться для каждого узла КЭМ. В результате расчета получается диаграмма изменения надежности по элементам конструкции.
Автор:
С.А. Пименов
Ведущий специалист по инженерным расчетам, компания NS Labs, к.т.н.
При копировании обязательна ссылка на сайт www.nslabs.ru
